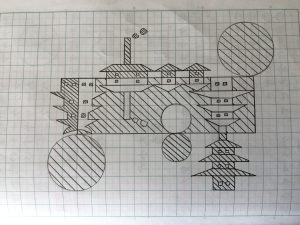
お知らせ
2022/02/28
4年生で、立方体や直方体の展開図が
幾通りもあることを経験しているので、
三角柱の展開図の学習でも辺と辺が
接する部分と底面や、
側面の形と数に気を付けて作図をしました。
今回は円柱の展開図ですが、子どもたちも
自信満々に「できます。」との声。
底面と側面の形と数に
気を付けて作図ができました。
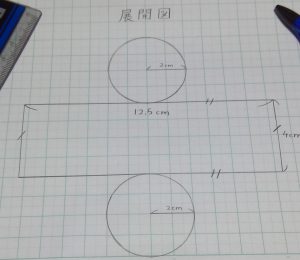
ただここで終わらないのが5年生、
前時の角柱の展開図と今回の円柱の展開図の
違いの考察に入ります。
教師(以下T)「三角柱の展開図の時と
少し様子が違うね、
底面と側面のくっつき方について
違いは捉えられますか。」
児童(以下C)「三角柱の時は辺と辺で
くっついていたけど、
円柱の底面と側面は、点でくっついています。」
C1「点でくっつくだけなのでAさんのような
展開図もいいけどBさんのような展開図でも
いいです。底面の円はどこでも。」
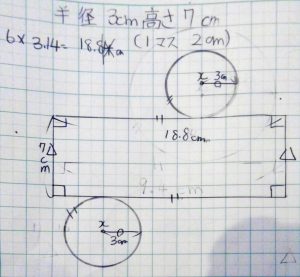
点でくっつくこと=底面の位置が
固定されないことの事実が確認できました。
ここまで児童の関心が高まってきたので、
T1「側面の形については、
みんな同じ長方形になるよね。」と
次に展開を考えて確認します。
C2「そうです。」
T2「じゃあ 例えばトイレットペーパーの
芯を開くと、長方形になるってことだよね。」
C3「そうです…あれ?」
「開いたら長方形にならなくて、こう、
ぐるっと巻いてるからちがう?」
(しばらく沈黙。
こういう間を大事にしたいです。)
C4「トイレットペーパーの芯開いたら、
平行四辺形になるよ。」
(生活経験と展開図の学習を
つなげる児童の発言が出てきます。)
C5「本当かなあ…
(タブレットの動画でたしかめて)
できてる!」
C6「じゃあ、これでもいいんですか?
だったら先生これはどうですか?」
アイデアを思い付いた児童は、
ノートに夢中でイメージを書きだします。
円柱の側面は曲面なので、
角柱と違って辺は存在しません。
ですから、切り開き方は自由です。
大人でも見落としがちな見方です。
友達の発言と、トイレットペーパーの
芯の具体例を受け止め、
次々に発想を広げていきました。
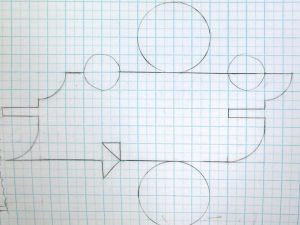
同じ知識でも、児童自らが柔軟な
見方・多様な考え方を働かせて
身に付けた知識は確かな力になると考えます。
最初に示した課題から、
児童それぞれが本気で考え始めた瞬間でした。
こういう時の子どもの笑顔は
算数の授業で大切にしたいです。
「今日の家庭学習の課題で、
できる人はオリジナル展開図を
続けて考えてみましょう。」
子どものチャレンジしたあしあとを紹介します。
(文:5年生 算数担当)